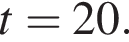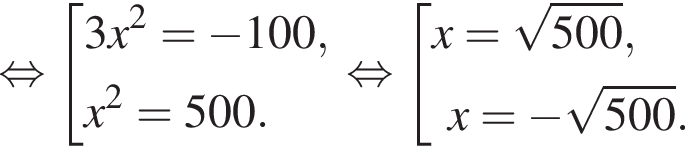На координатной прямой отмечены точки А, В, С, D, E. Если расстояние между A и С равно ![]() то ближе других к точке с координатой 0,5 расположена точка:
то ближе других к точке с координатой 0,5 расположена точка:
На рисунке изображен треугольник ABC, в котором ∠ACB = 41°, ∠AMN = 107°. Используя данные рисунка, найдите градусную меру угла BAC.
Используя рисунок, определите верное утверждение и укажите его номер.


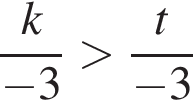
Результат разложения многочлена x (a − 6b) + 6b − a на множители имеет вид:
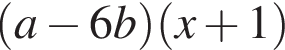
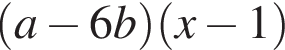
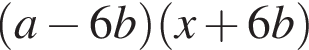
Из точки А к окружности проведены касательные AB и АС и секущая AM, проходящая через центр окружности О. Точки В, С, M лежат на окружности (см. рис.). Найдите величину угла AOB, если

Величины a и b являются прямо пропорциональными. Используя данные таблицы, найдите неизвестное значение величины a.
| a | 1,3 | |
| b | 116 | 5,2 |
Точки A, B, C разделили окружность так, что градусные меры дуг AB, BC, CA в указанном порядке находятся в отношении 5 : 6 : 7. Найдите градусную меру угла ABC.
Среди данных утверждений укажите номер верного.
Результат упрощения выражения 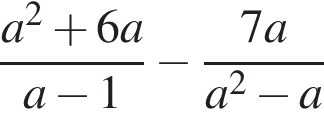 имеет вид:
имеет вид:
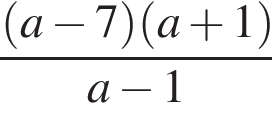
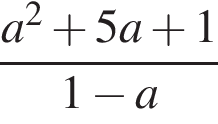
Прямая a пересекает плоскость α в точке A и образует с плоскостью угол 60°. Точка B лежит на прямой a, причем AB = ![]() Найдите расстояние от точки B до плоскости α.
Найдите расстояние от точки B до плоскости α.
Укажите область значений функции
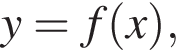 заданной графиком на промежутке [−2; 4] (см. рис.).
заданной графиком на промежутке [−2; 4] (см. рис.).
Упростите выражение 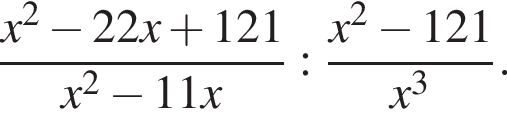
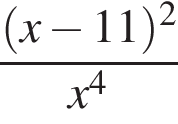
Найдите значение выражения 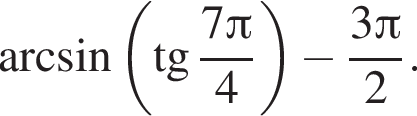
Известно, что наименьшее значение функции, заданной формулой y = x2 + 12x + c, равно −11. Тогда значение c равно:
Найдите сумму целых решений неравенства 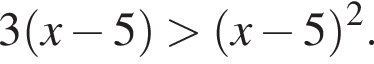
В ромб площадью ![]() вписан круг площадью 5π. Сторона ромба равна:
вписан круг площадью 5π. Сторона ромба равна:
График функции, заданной формулой y = kx + b, симметричен относительно оси Oy и проходит через точку A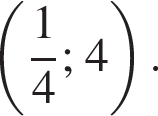 Значение выражения k + b равно:
Значение выражения k + b равно:
Сумма всех натуральных решений неравенства  равна:
равна:
Найдите сумму всех целых решений неравенства 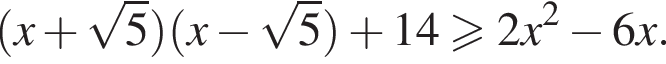
На рисунках 1 и 2 изображены правильная треугольная призма ABCA1B1C1 и ее развертка. Найдите площадь боковой поверхности призмы, если длина ломаной ACA1 равна ![]() и точки A, C, A1 лежат на одной прямой (см. рис. 2).
и точки A, C, A1 лежат на одной прямой (см. рис. 2).
Найдите сумму целых решений (решение, если оно единственное) системы неравенств 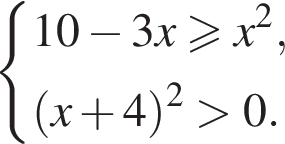
Найдите произведение большего корня на количество корней уравнения 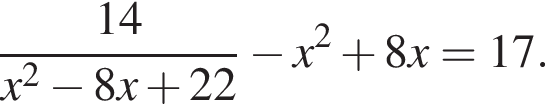
В равнобедренную трапецию, площадь которой равна ![]() вписана окружность. Сумма двух углов трапеции равна 60°. Найдите периметр трапеции.
вписана окружность. Сумма двух углов трапеции равна 60°. Найдите периметр трапеции.
Найдите сумму целых решений неравенства 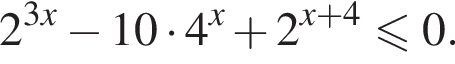
Найдите наибольшее целое решение неравенства 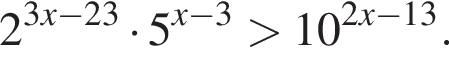
Найдите
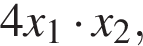 где
где ![]() — абсциссы точек пересечения параболы и горизонтальной прямой (см.рис.).
— абсциссы точек пересечения параболы и горизонтальной прямой (см.рис.).
Четырёхугольник ABCD вписан в окружность. Если 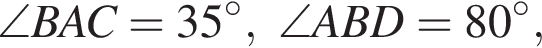 то градусная мера между прямыми AB и CD равна ...
то градусная мера между прямыми AB и CD равна ...
Найдите (в градусах) наибольший отрицательный корень уравнения 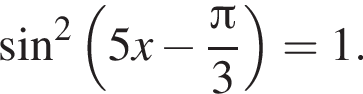
Из города А в город В, расстояние между которыми 140 км, одновременно выезжают два автомобиля. Скорость первого автомобиля на 10 км/ч больше скорости второго, но он делает в пути остановку на 20 мин. Найдите наибольшее значение скорости (в км/ч) первого автомобиля, при движении с которой он прибудет в В не позже второго.
Найдите произведение наибольшего целого решения на количество целых решений неравенства 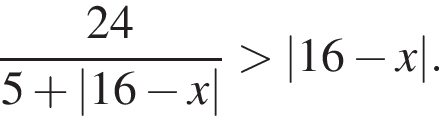
Из двух растворов с различным процентным содержанием спирта массой 450 г и 300 г отлили по одинаковому количеству раствора. Каждый из отлитых растворов долили в остаток другого раствора, после чего процентное содержание спирта в обоих растворах стало одинаковым. Найдите, сколько раствора (в граммах) было отлито из каждого раствора.
Найдите произведение корней уравнения 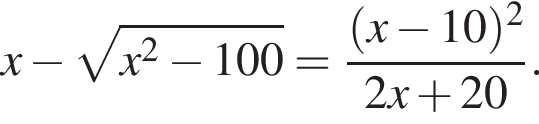

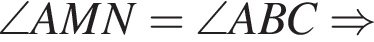
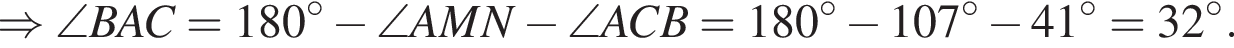
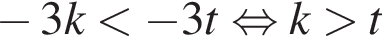 — неверно.
— неверно.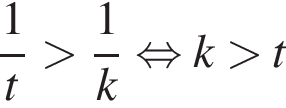 — неверно.
— неверно.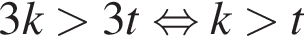 — неверно.
— неверно.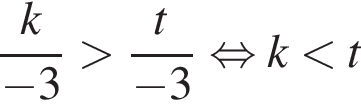 — верно.
— верно.
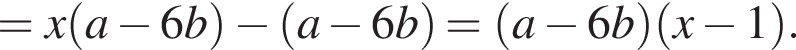

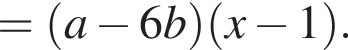
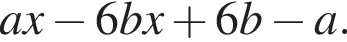
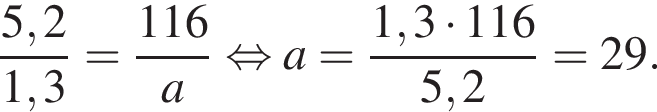
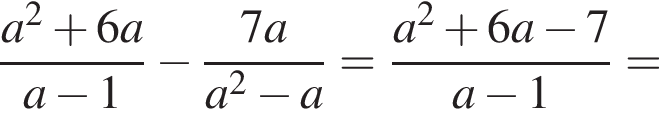
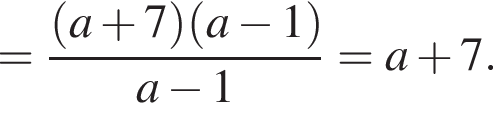
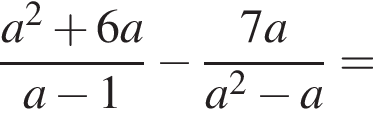
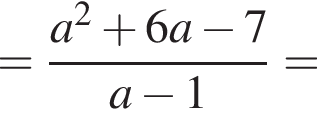

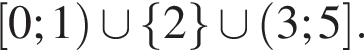
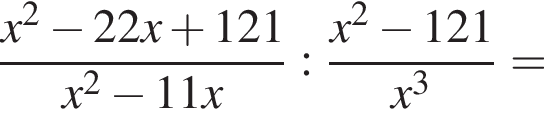
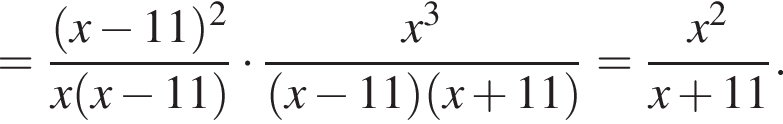
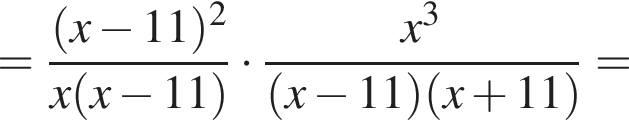
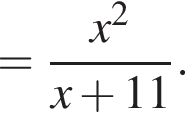
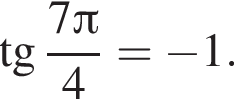 Поэтому:
Поэтому: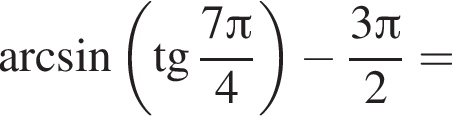
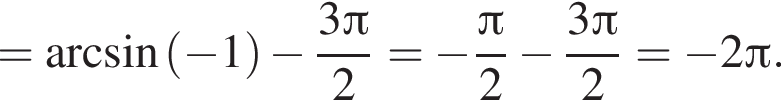
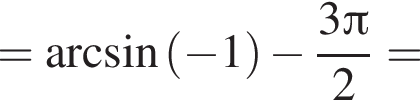
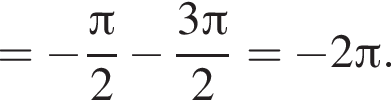
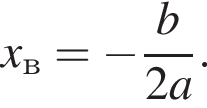 Поэтому
Поэтому 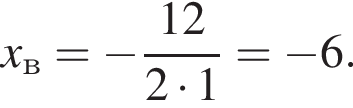 Поскольку y(xв) = −11, имеем:
Поскольку y(xв) = −11, имеем: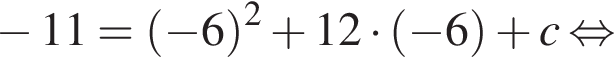


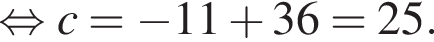
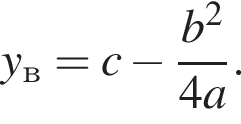
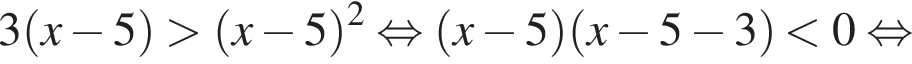

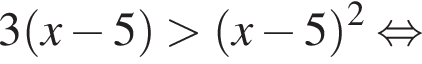
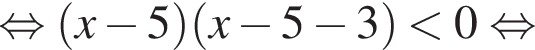
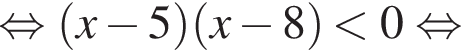

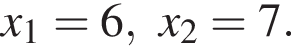 Их сумма равна:
Их сумма равна: 
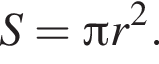 Следовательно, радиус круга равен:
Следовательно, радиус круга равен: 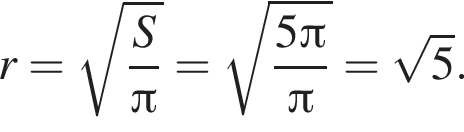 Площадь ромба равна произведению высоты на его сторону:
Площадь ромба равна произведению высоты на его сторону:  Тогда:
Тогда: 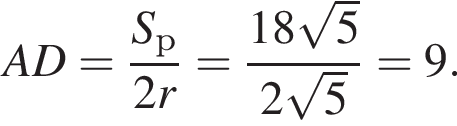
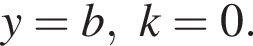 Прямая проходит через точку A с координатами
Прямая проходит через точку A с координатами 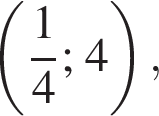 отсюда b = 4. Поэтому k + b = 4.
отсюда b = 4. Поэтому k + b = 4.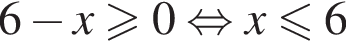 и
и  следовательно, натуральные решения неравенства: 1, 2, 3, 4, 5, 6, 17. Их сумма равна 38.
следовательно, натуральные решения неравенства: 1, 2, 3, 4, 5, 6, 17. Их сумма равна 38.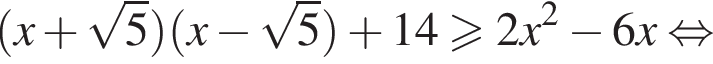
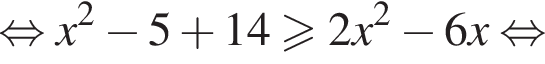
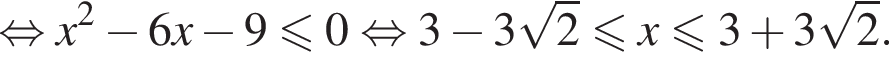
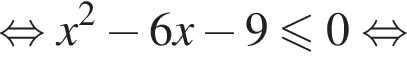
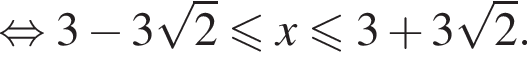
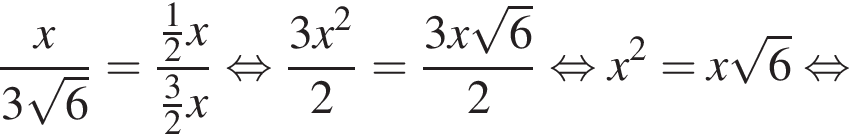
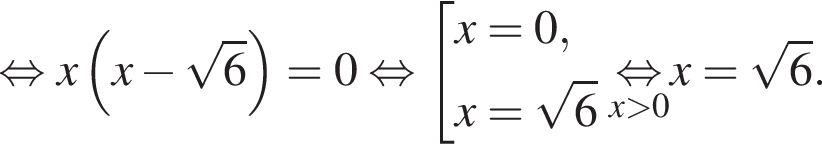
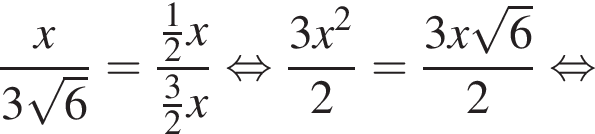
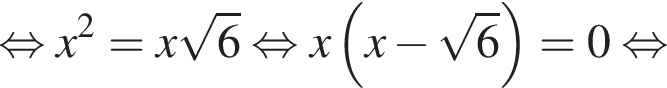
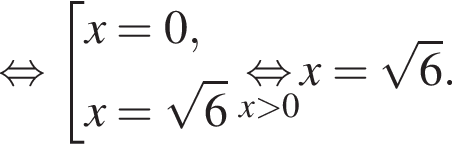
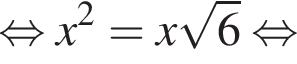
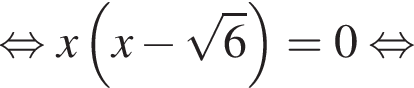
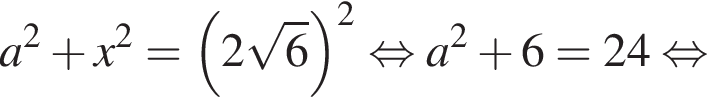

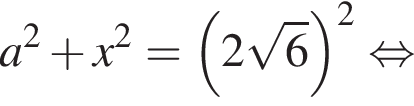
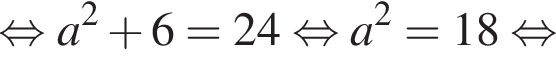
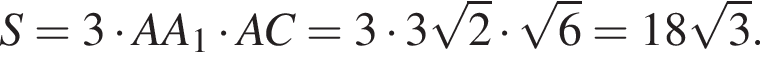

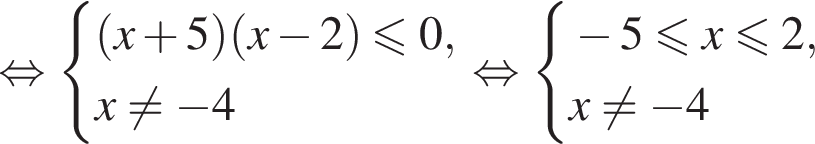
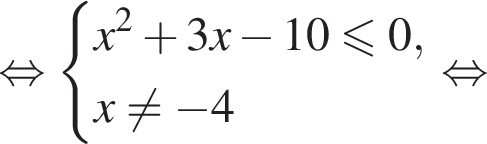
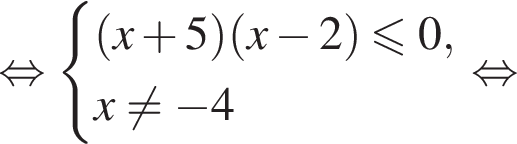
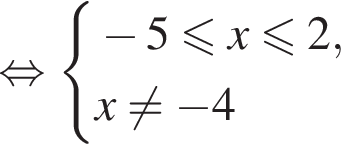
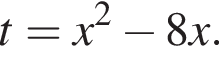 Тогда:
Тогда: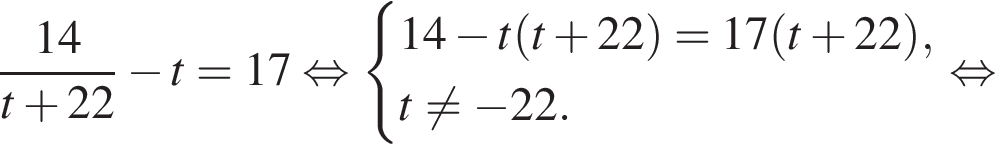
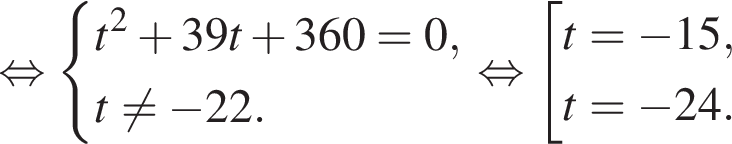
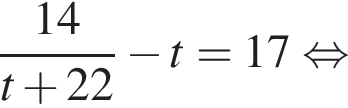
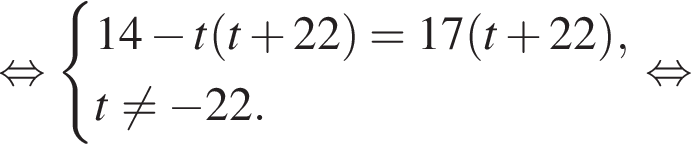
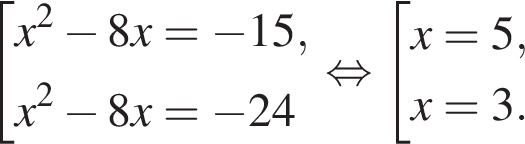
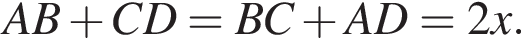 Сумма углов в равнобедренной трапеции, прилежащих к одной стороне равна 180°, откуда следует, что сумма углов, данная в условии — есть сумма углов при основании AD, которые равны.
Сумма углов в равнобедренной трапеции, прилежащих к одной стороне равна 180°, откуда следует, что сумма углов, данная в условии — есть сумма углов при основании AD, которые равны. 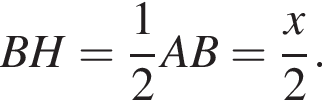 Поэтому из площади трапеции найдем x:
Поэтому из площади трапеции найдем x: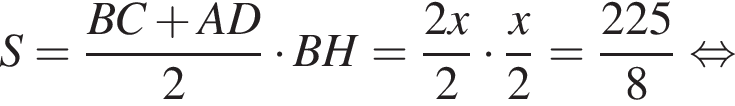
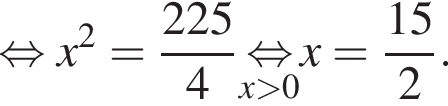
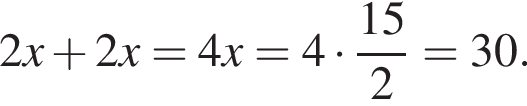
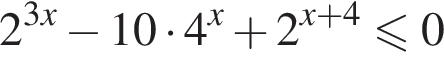
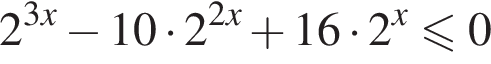
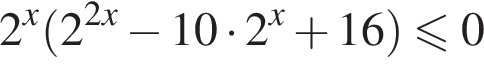
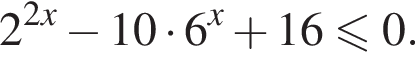
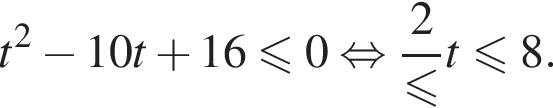
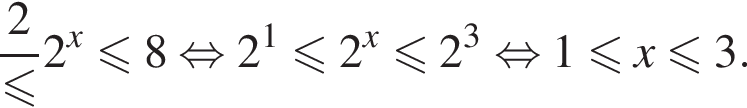
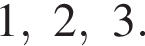 Их сумма равна 6.
Их сумма равна 6.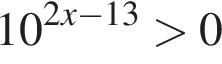 :
: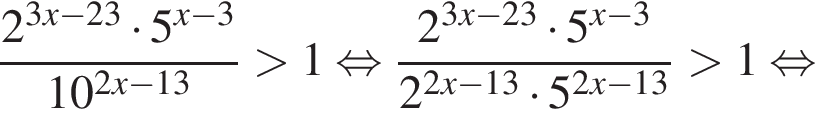
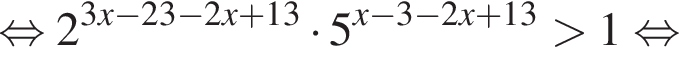
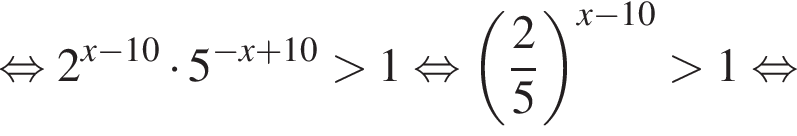
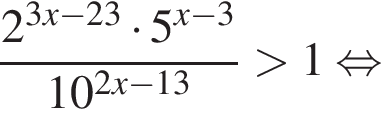
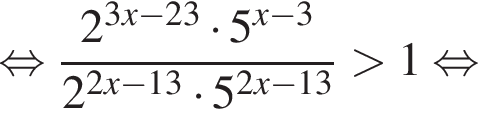

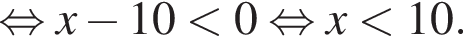
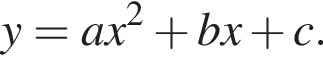 На рисунке изображена парабола с ветвями, направленными вверх, следовательно,
На рисунке изображена парабола с ветвями, направленными вверх, следовательно, 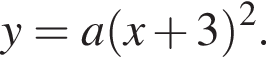 Для того, чтобы найти a, подставим в уравнение параболы точку (-2;1), через которую данная парабола проходит:
Для того, чтобы найти a, подставим в уравнение параболы точку (-2;1), через которую данная парабола проходит: 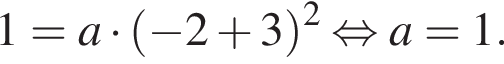 Таким образом, изображённая на графике парабола задается уравнением
Таким образом, изображённая на графике парабола задается уравнением 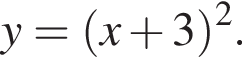
 :
: 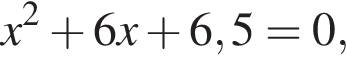 откуда по теореме Виета
откуда по теореме Виета 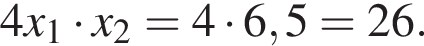





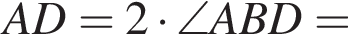
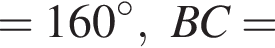
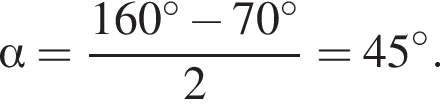
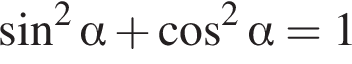 :
: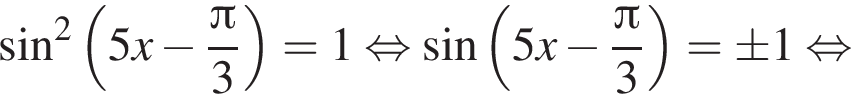
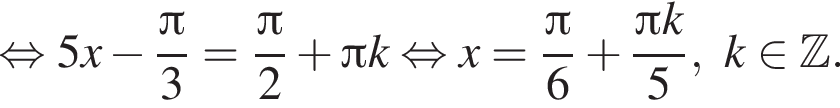
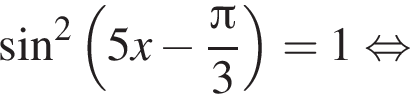
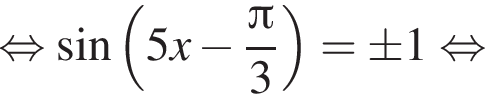
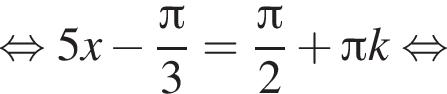
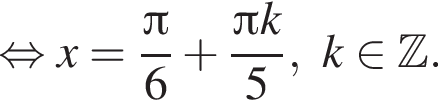
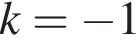 и равен
и равен 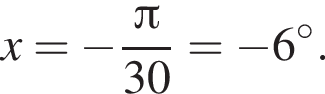
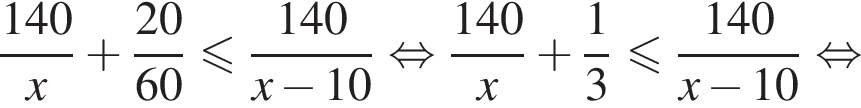

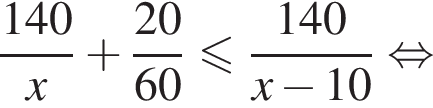
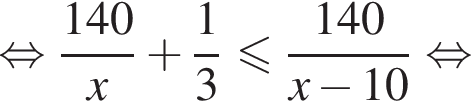
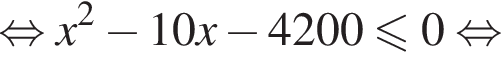

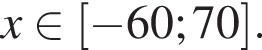 Таким образом, наибольшее значение скорости первого автомобиля — 70 км/ч.
Таким образом, наибольшее значение скорости первого автомобиля — 70 км/ч.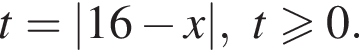 Имеем:
Имеем: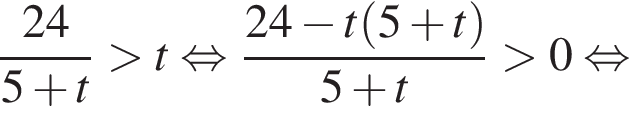
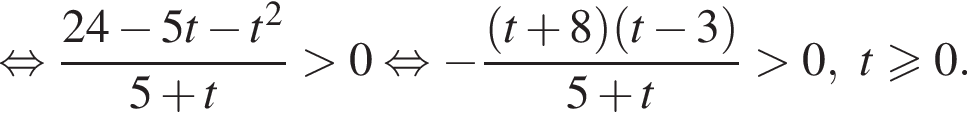
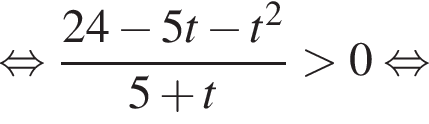
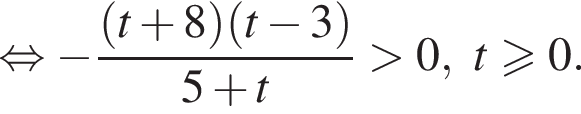
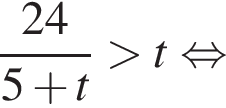
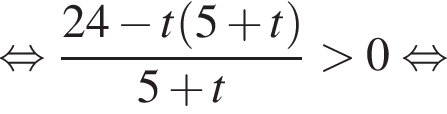
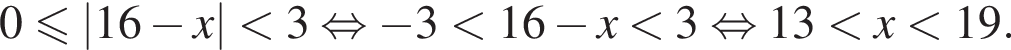
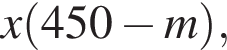 во втором —
во втором — 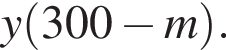 После переливания масса спирта в 1-ом сосуде равна
После переливания масса спирта в 1-ом сосуде равна 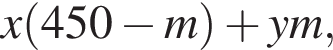 во втором —
во втором —  Так как концентрации стали одинаковыми, а объёмы относятся как 3:2, во втором сосуде в 1,5 раза меньше спирта. Тогда:
Так как концентрации стали одинаковыми, а объёмы относятся как 3:2, во втором сосуде в 1,5 раза меньше спирта. Тогда: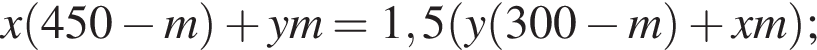
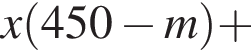


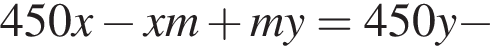
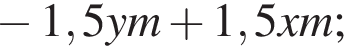
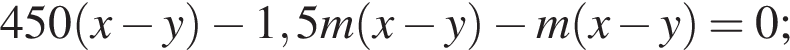

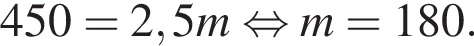
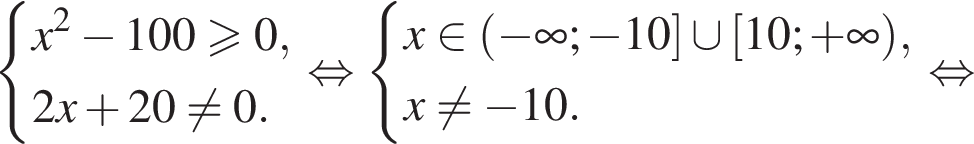
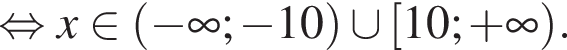
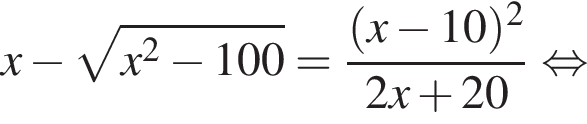
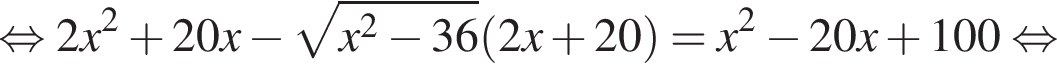
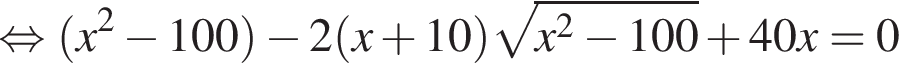
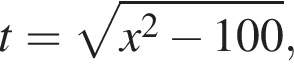 тогда
тогда 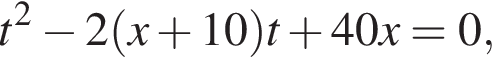 откуда
откуда 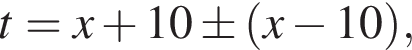 то есть
то есть